物理ベースレンダリングの「光」について基礎的な部分がアニメーションでよくわかる「Physically based rendering from first principles」

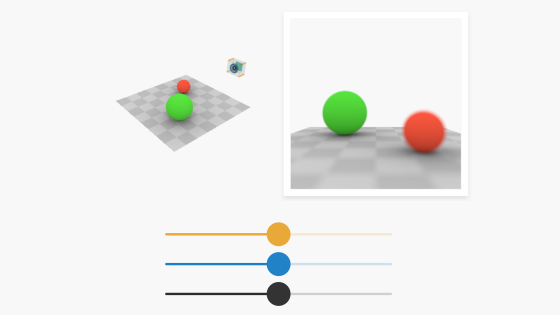
CGでリアルな質感を表現するためには、物理ベースレンダリングによる光と物体との相互作用のシミュレートが必須となります。光の基本的な性質から物体表面の光の反射についてどのような計算が行われているかの基礎をアニメーションでわかりやすく解説したサイトが公開されています。

Physically based rendering from first principles
https://imadr.me/pbr/

◆第1章：光とは何か？
光は波なのか粒子なのかどちらか一方を仮定すると相反する現象が確認されるという謎がありましたが、現代では量子電磁力学が光と物質のあらゆる相互作用を記述する最も正確な理論として認知されています。サイトではどのような理論がどの光の現象に対応しているかを、マウスを重ねることで調べることができます。

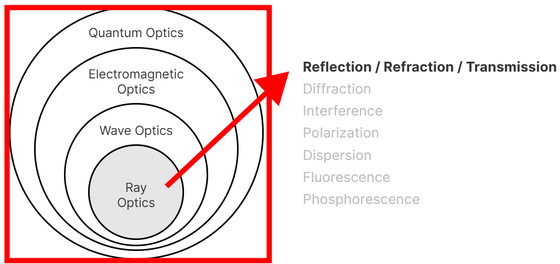
物理ベースレンダリングで光の相互作用をシミュレートするには幾何光学を利用しますが、前半は予備知識と他の理論も一部含めて光とは何かについて解説しています。

◆電気力
電荷は正と負の2種類があり、同じ種類の電荷は互いに反発し、反対の電荷は引き合います。2つの荷電粒子に作用する力の量は、クーロンの法則を使用して計算されます。kは定数・q1とq2は各電荷の量、rはそれらの間の距離です。

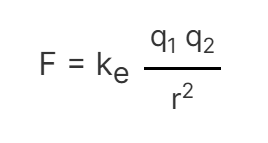
電荷を移動させると電気力がどのように影響するかを、サイトでは実際に動かして矢印の向きと大きさで把握することができます。

電荷によって生み出される電場のイメージはこんな感じ。

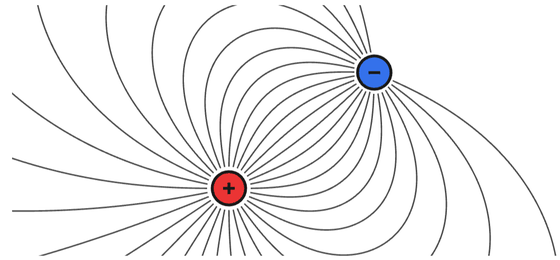
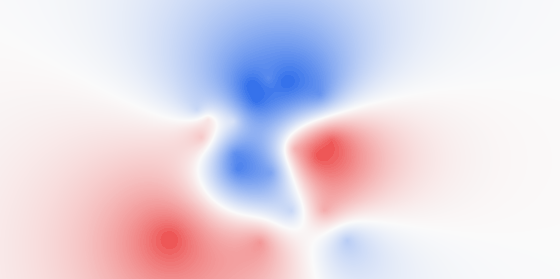
色のグラデーションで電場を表したイメージはアニメーション化されています。

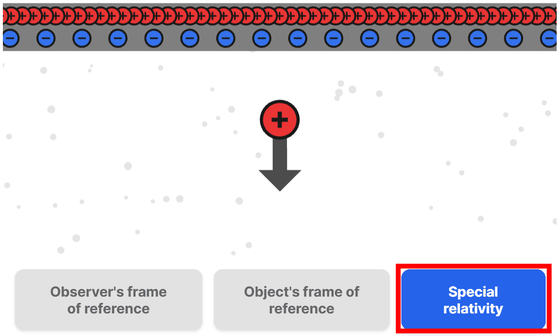
◆特殊相対性理論と磁気
サイトでは観察者および正電荷自身から見た電荷の動きと特殊相対性理論による電荷への力の発生、すなわち磁気についてアニメーションで把握することができます。

◆マクスウェル方程式
電場と磁場がどのように生成され相互に作用するかは、マクスウェル方程式で表されます。バーを動かしコイル内の磁石を動かすと変化する磁場によりワイヤに電流が誘導されるというマクスウェルの第3方程式すなわちファラデーの電磁誘導の法則を視覚的に把握できます。

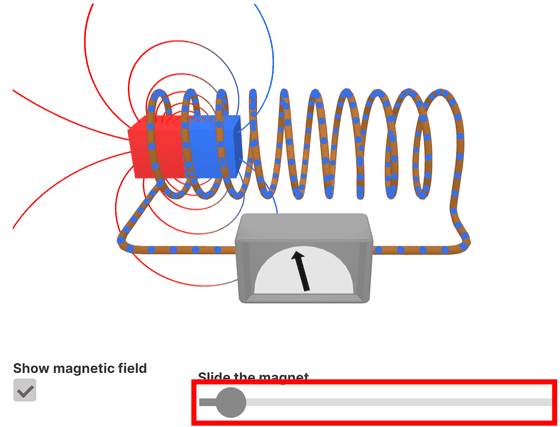
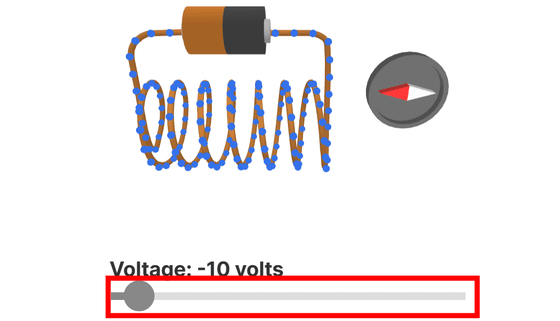
マクスウェルの第4方程式であるアンペールの法則により、コイルに電流を流すと磁場が発生します。バーを動かすと電圧が変わり、電流の向きによって磁場が変わります。

◆電磁波
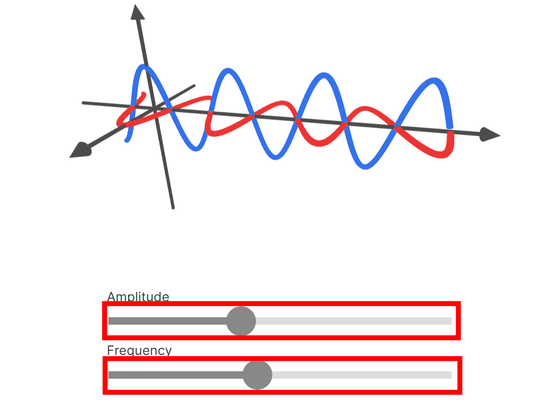
電場と磁場が同期して発生する波を電磁波といい、真空中では光速で移動します。波の振幅は電場または磁場の最大強度、つまり光子の量を表し、周波数は光子のエネルギーに対応します。バーを動かすと振幅と周波数によって電磁波の波長が変化します。

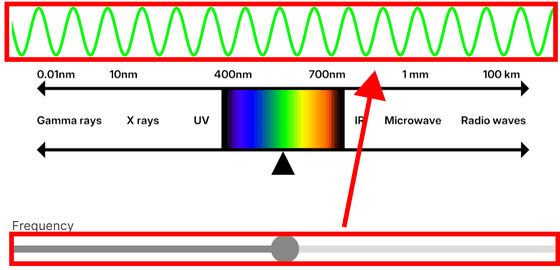
波長が約400nmから700nmの間にあるとき、人間の目はそれを可視光として知覚します。バーを動かすと電磁波の周波数と色が変化します。

◆光の生成
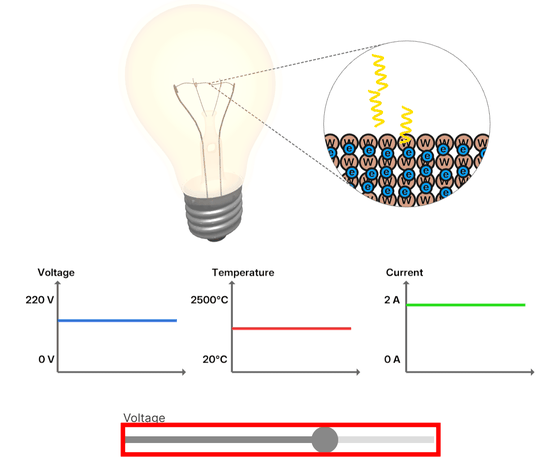
白熱電球に電流を流すとフィラメントの抵抗により熱が発生し、フィラメント内の電子が揺れ動き衝突する過程で光子を放出します。この光の放射は黒体放射として分類されます。サイトではバーを動かし電圧を変えることで、温度変化や電球から光が発生する過程を視覚的に把握できます。

太陽から発せられる光は、白熱電球とは異なり核融合反応によって生成されます。太陽の核では水素原子核が融合してヘリウムを形成し、ガンマ線として光子を放出します。太陽から放射される電磁波のうち約49％は赤外線、約43％は可視光となり残りの約8％は紫外線となります。

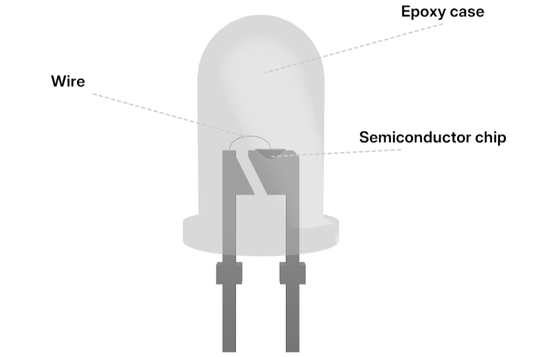
LEDではP型半導体とN型半導体を並べて電流を流すと電界発光により光が生成されます。

その他の光源については、Wikiのルミネセンスにまとめられています。

◆第2章：光の抽象化
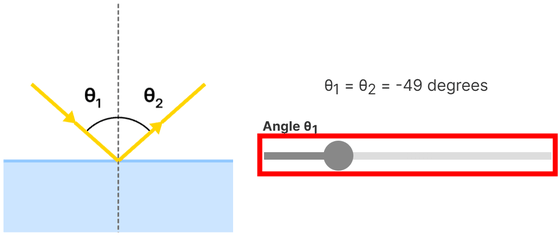
光子が物体に当たると、反射もしくは屈折のいずれかの事象が起こります。反射の法則に従い反射角は表面の法線に対する入射角に等しくなります。バーを動かすと入射角に合わせて反射角が変化します。

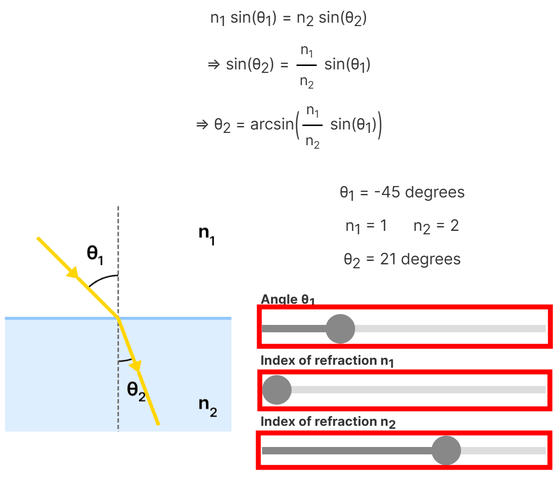
屈折角は屈折率からスネルの法則を使用して計算されます。光の入射角θ1とn1・n2それぞれの屈折率から屈折角θ2がどう変化するかそれぞれのバーを動かすことで視覚的に把握できます。

反射および屈折する光の量はフレネルの方程式から求められますが、フレネル方程式全体をリアルタイムで計算すると時間がかかる可能性があるため、1994年にクリストフ・シュリック氏が近似式を考案しました。

まず、法線から0度での反射率を計算します。

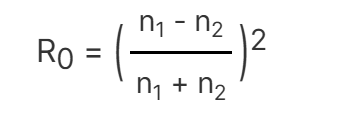
次に、反射率の近似関数にR0を代入します。

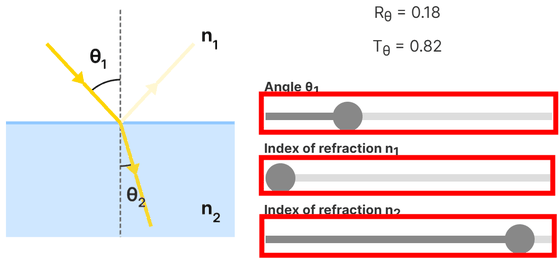
反射した光の大きさRθから透過した光の大きさTθは「Tθ＝1-Rθ」で求められます。光の入射角θ1とn1・n2それぞれの屈折率をバーで変化させると、反射する光の大きさと透過する光の大きさが求められ図に反映されます。

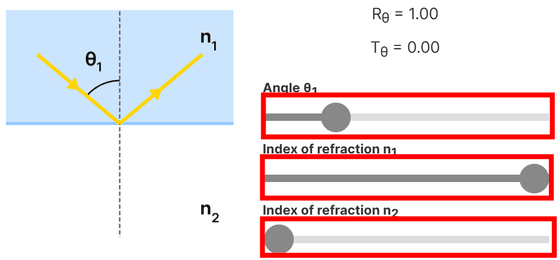
全ての光が反射される現象を全反射と呼びます。

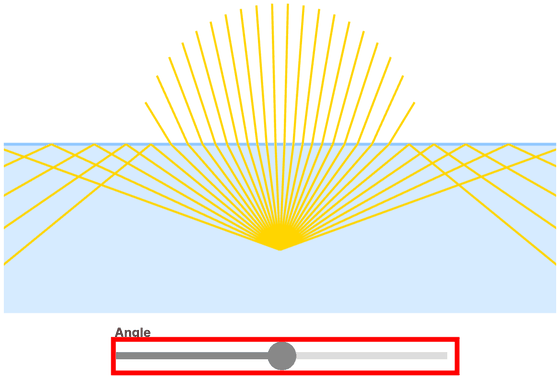
全反射はスネルの窓と呼ばれる現象を引き起こします。サイトの図では黄色の線が集中している場所を視点とし、どのような光が集まって見えるかを表したもので、バーを動かすと視点の角度が変化し、どの方向の光を見ることができるかが分かります。

水中に潜って上を見ると、表面上の光は96度の幅の円形の窓を通して屈折し、このように見えます。

◆マイクロファセットモデル
10億分の1メートルを基準としたナノジオメトリの場合は、光が表面で回折する光波として物質と相互作用することを波動光学を用いて説明できます。範囲を広げて100万分の1メートルを基準としたマイクロジオメトリの場合は、光を表面の反射および屈折する直線光線と見なす幾何光学を用いて説明できます。よって、反射の法則・スネルの法則・フレネル方程式が使用できます。

コンピューターグラフィックのレンダリングでは、さらに範囲を広げて1ピクセル単位で考慮する必要があります。それぞれのピクセルをマイクロ単位の無数の微細な凹凸がある表面が含まれるマイクロファセットモデルとして扱い、統計的平均を使用してそのピクセルでの表面の外観をシミュレートします。

マイクロファセットモデルの法線は粗くなるにつれて整列しなくなります。バーを動かすと表面の粗さを変化でき、粗くなることで光の反射方向が乱れることが分かります。

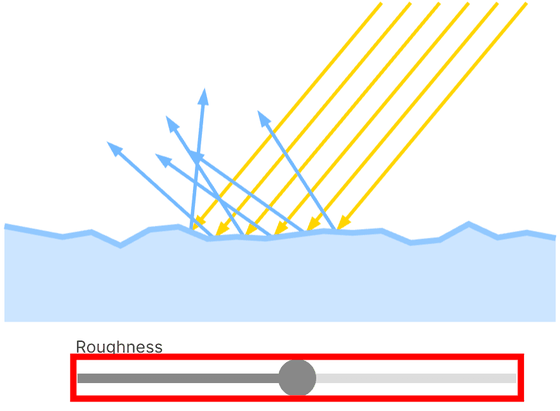
さらに表面が粗くなるほど光線が円錐上に広がる性質があり、この円錐の大きさは双方向反射率分布関数で求められます。バーを動かし表面が粗くなるほど円錐が広がる様子を把握可能です。

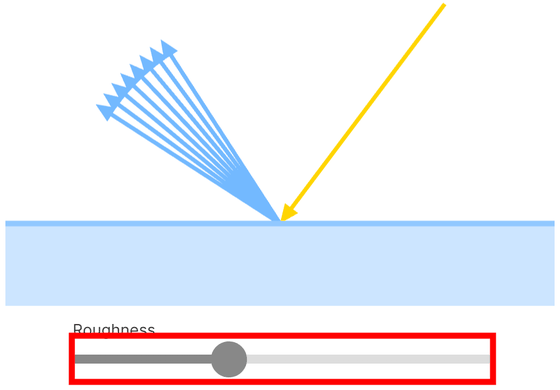
ここで、マイクロファセットモデルを金属と非金属の2種類に区別します。

◆金属
金属の場合、光子が表面から数ナノメートル入ると自由電子によって簡単に吸収されます。吸収されない光は可視光スペクトル全体で均等に反射され、独特の銀系の灰色を生み出します。例外として、金・銅・オスミウム・セシウムの場合は特定の波長を吸収するため、独特の色を発生させます。

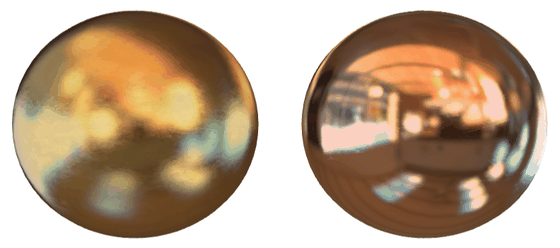
金属の表面の粗さを変えると鏡面反射は変化しますが、反射する光以外の光子は吸収されるため拡散反射は起こりません。バーを動かし表面の粗さを変えると、鏡面反射は変化するが拡散反射は起こらないということが確認できます。

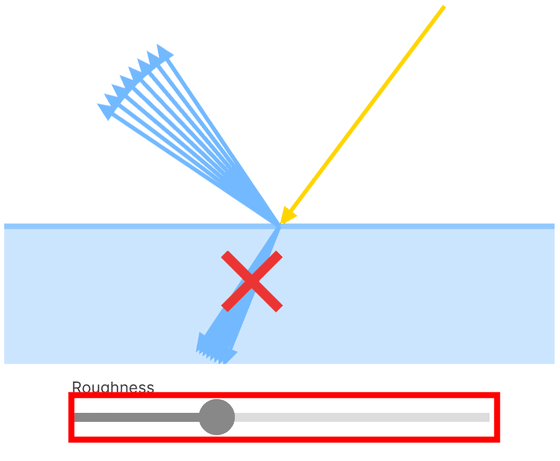
◆非金属
非金属はプラスチック・木材・ガラス・水・ダイヤモンド・空気など誘電体と呼ばれる電気を通さない物体が属します。

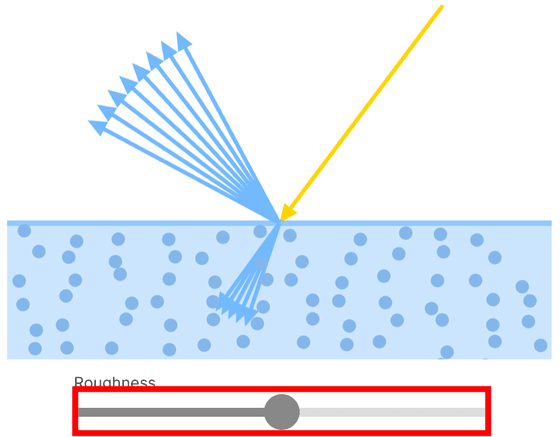
光子が誘電体に当たると、そのエネルギーが対象内の電子のエネルギーと一致する場合にのみ吸収され、一致しない場合は鏡面反射が起こります。さらに拡散反射と呼ばれる現象が起こり、光は誘電体材料内で屈折し材料内の色素と相互作用しながら跳ね回り表面から出ます。表面の粗さにより、鏡面反射と拡散反射が変化します。バーを動かし表面の粗さを変えると、鏡面反射と拡散反射が変化する様子を確認できます。

◆分光分布
赤いリンゴにすべての可視波長を含む白色光を当てると、リンゴの色素であるアントシアニンが紫、青、緑の波長などのほとんどの波長を吸収し、色の強度を減少させます。残りの波長のうち赤は、リンゴの表面から散乱されることでリンゴを赤として知覚させます。

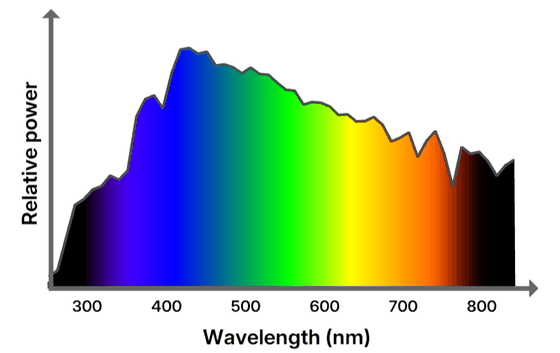
入射光を各波長で運ぶエネルギーの量を関数を使用して分光分布またはSPDとしてグラフで表すことができます。例えば、以下は国際照明委員会（CIE）によって標準化された理論的な光源D65のSPDで、西ヨーロッパまたは北アメリカの平均的な正午の光のスペクトルを表しています。

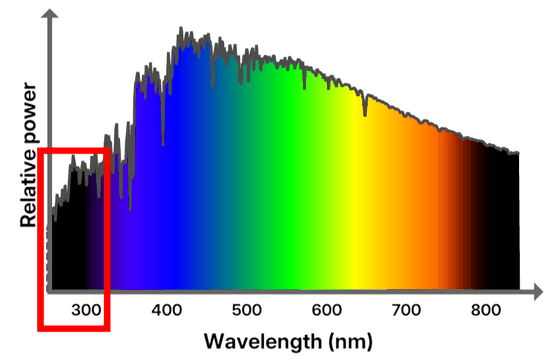
地球の大気に入る前の宇宙空間で測定された太陽放射AM0のSPDと比較すると、AM0では紫外線範囲の落ち込みがないことが分かります。

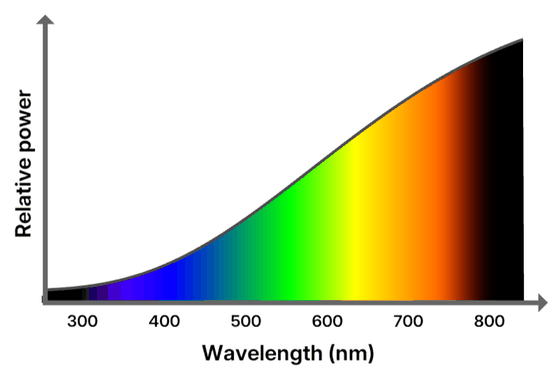
タングステン白熱灯のSPDは以下のようになります。

◆分光反射率曲線
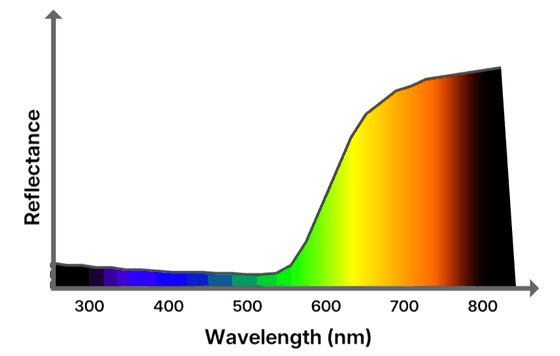
SPDは光源がどれだけの色で構成されているかを示します。対して、物体によって反射される入射光の割合を示す分光反射率曲線では、事実上その物体の色を表します。赤いリンゴの場合、赤の波長でほとんどの光を反射するため、その分光反射率曲線は次のようになります。

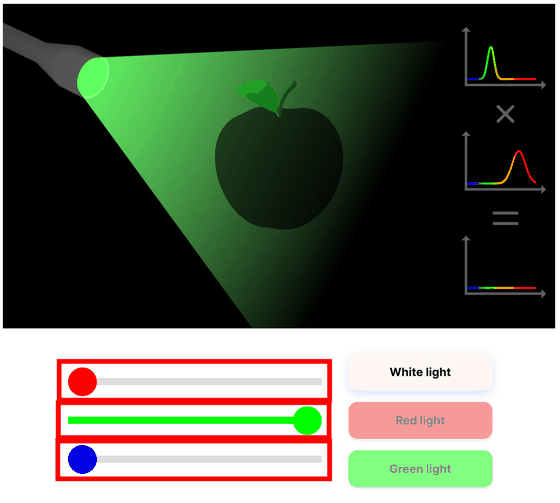
物体の色がどのように見えるかは、光源の分光分布と物体の分光反射率の組み合わせで得られる結果となります。赤いリンゴに白色光を当てるとリンゴは赤く見え、赤い光でも同じ結果が得られます。しかし、緑色の光を当てると葉以外のリンゴの残りの部分は光を反射せず黒く見えます。サイトでは懐中電灯から発せられる赤・緑・青それぞれの光の強さを調整するバーがあり、SPDによって赤いリンゴがどのように見えるか確認できます。

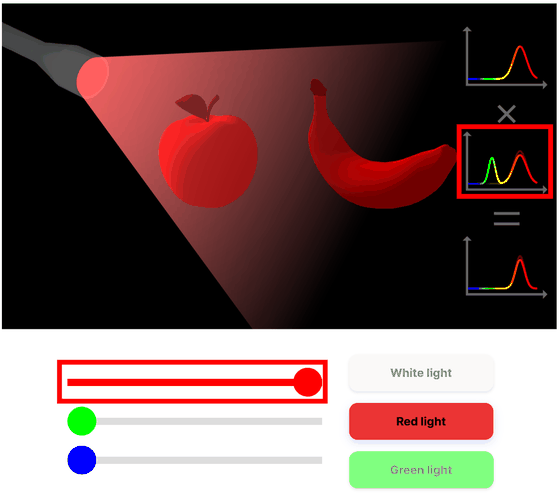
白色光の元でバナナが黄色に見えるのは、緑と赤を反射して得られる合成色が黄色であるためです。赤色だけの照明を当てるとバナナは赤色のみ反射することになるので、赤みがかって見えます。赤色のリンゴと黄色いバナナが赤色の照明の元では、同じ赤色に見えるこの現象を条件等色と呼びます。

◆第3章：レンダリング方程式
物理ベースレンダリングで利用されるレンダリング方程式の1例です。

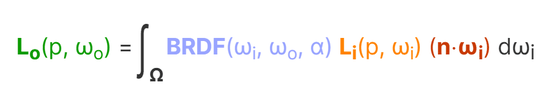
・Lo(p,ωo)：点pから方向ωoへの出射光
・Li(p,ωi)：方向ωiから点pへの入射光
・双方向反射率分布関数BRDF：入射光Li(p,ωi)のうちどれだけが点pで出射方向ωoに反射されるかを示す関数で材質を示します。
・ドット積：余弦項

レンダリング方程式は半球Ωの方向ωiから来るすべての入射光Liを、その点でのBRDFと余弦項で重み付けして合計することにより、点pで方向ωoに向かって反射される出射光Loを導き出します。

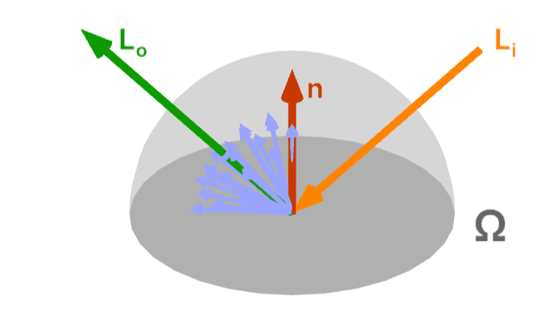
このレンダリング方程式を項目ごとに分けて説明していきます。

◆ランベルトの余弦則
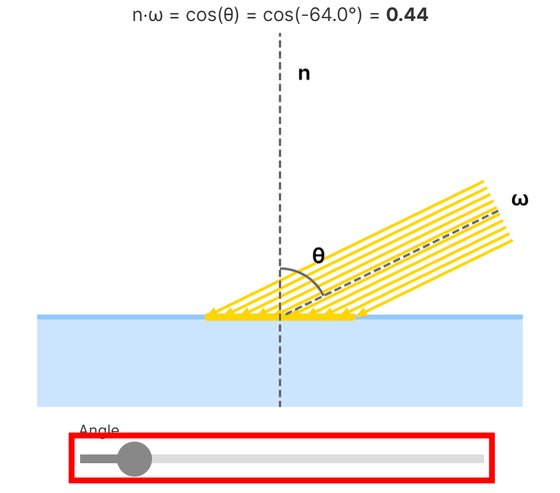
ランベルトの余弦則より、光線の入射角が垂直だと接触する表面積は狭く、角度が斜めになるほど面積が広がります。バーを動かし角度を変えることで、表面に当たる面積が変化します。

◆双方向反射率分布関数BRDF
BRDFはレンダリング方程式の最も重要な部分で、材料の表面とその外観を表します。ここでマイクロファセット理論とエネルギー保存を適用して、レンダリングモデルを物理ベースにすることができます。入射光の方向ωiと出射光の方向ωo、および表面の粗さをα、拡散反射成分と鏡面反射成分にそれぞれの係数kdとksで重み付けされた値を表します。

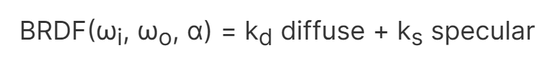
BRDFは多くの種類がありますが、リアルタイムレンダリングで最も一般的なのはthe Cook-Torrance鏡面マイクロファセットモデルとランベルト拡散モデルを組み合わせたものです。

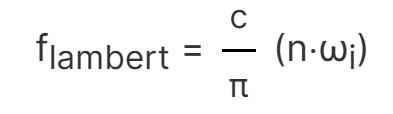
ランベルト拡散成分はアルベドと呼ばれる拡散色に余弦係数を掛けたものですが、レンダリング方程式にすでに余弦係数があるため、求める式は次のようになります。Dは法線分布関数、Fはフレネル方程式、Gは幾何関数です。

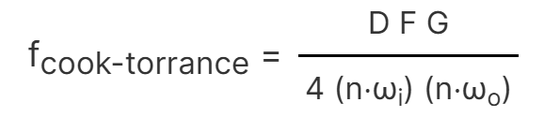
◆正規分布関数
正規分布関数とは入射方向ωiから反射して出射方向ωoに向かう光を反射するように配向した微小面の数を近似的に表現する関数で、今回はTrowbridge-Reitz GGX関数を使用します。

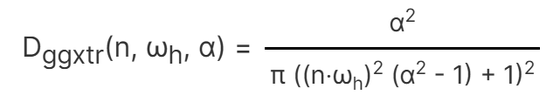
ωhは入射方向と出射方向の間のハーフベクトルで、次のような式になります。

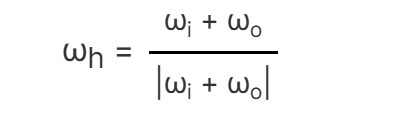
サイトではバーを動かすと表面の粗さが変化し、微小面の数が変化する様子を確認できます。

◆幾何関数
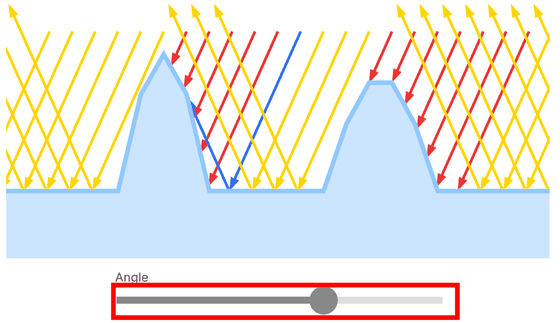
下の図の赤色の入射光線は、出射方向に跳ね返ることができないシャドーイングと呼ばれる状態です。青色の入射光線は出射方向に向かう途中で遮蔽されておりマスキングと呼ばれる状態となっています。バーを動かすと入射光線の角度が変わり、赤色のシャドーイング状態の光や青色のマスキング状態の光が変化します。

これらの効果を幾何関数により近似的に表現します。ここではSchlick-GGX幾何関数を使用します。

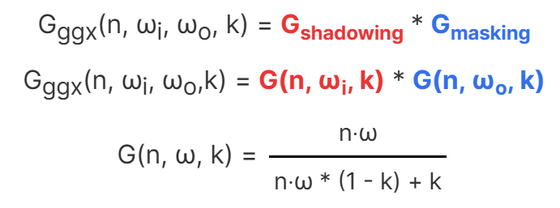
kの値は以下の通りです。

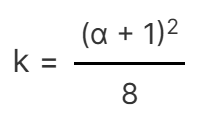
バーを動かすと表面の粗さが変わり、シャドーイングとマスキングの効果が変わります。

◆フレネル方程式
リアルタイムレンダリングにおいては、高速で十分な精度のシュリック氏の近似式を使用します。

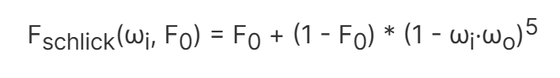
バーを動かすと反射率が変わり反射される光の強さの変化が確認できます。

◆すべてを組み合わせる
以上の式を組み合わせて、物理ベースレンダリングを行います。サイトではバーで表面の粗さと金属値およびベースカラーを変更することで、レンダリング結果を視覚化できます。

球の表面の粗さと金属値の相関関係を示す表は次のとおりです。

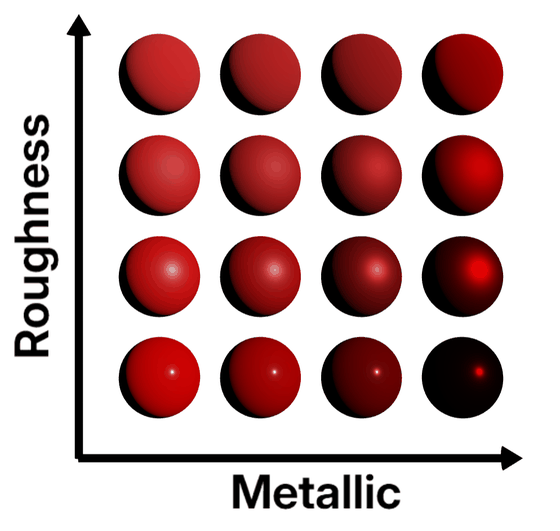
通常、金属値は0または1のいずれかですが、物理ベースレンダリングでは中間値を考慮して、金属と非金属の間をスムーズに補間することが実用的です。錆びた金属材料を表現する際に利用できます。

なお、サイトでの説明は基礎部分となり、将来的にはボリュームレンダリング、サブサーフェススキャタリング、光学分散、薄膜干渉・虹色などの効果をカバーするとのことです。