3D空間で物体をらせん状に移動させるには？

3D空間における物体の動きを表現するには数学の理解が必要となります。「Moving Objects in 3D Space」は、丸い球体に沿ってらせん状に動くような点の軌跡を数学的にどうやって表現するのかをアニメーション付きのスライドで解説してくれるサイトです。

Moving Objects in 3D Space
https://visualrambling.space/moving-objects-in-3d/

3D空間でらせんを描く時、「球体の表面を移動する点」をイメージするとわかりやすくなります。なお、Moving Objects in 3D Spaceでは、アニメーションも用いて説明が行われ、画面右側をクリックあるいはタップするとスライドが進み、左側をクリッククリックあるいはタップするとスライドが戻ります。

3D空間を3次元直交座標系と捉え、点の動きをX・Y・Zに分解して考えます。例えば、X=10cos(πt/2)と表現します。tは媒介変数です。Xはシンプルな余弦関数なので、以下のようにきれいな波になります。

Yも同じく10*cos(πt/2)と表現するとこんな感じ。

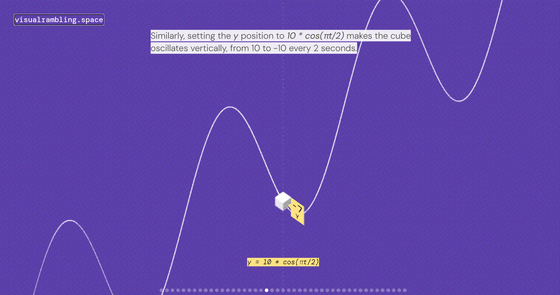
点(X, Y)の軌跡で円を表現するには、このようにXとYを三角関数で表現する必要があります。

ただし、円を表現する場合は、X=10cos(πt/2)に対してY＝10*sin(πt/2)にします。これで点(X, Y)は半径10の円を描きます

次に、X＝10cos(πt/2)×0.03tとしてみます。この関数だと、以下のようにどんどん波の振幅が大きくなっていく動きになります。

Y＝10sin(πt/2)×0.03tでも同じこと。

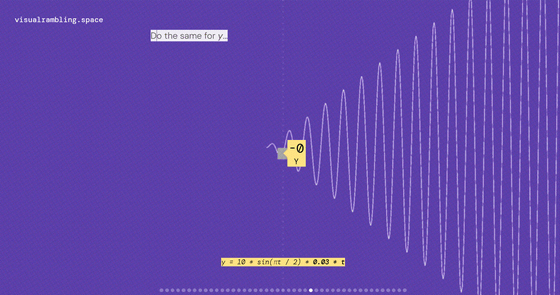
(X, Y)＝( 10cos(πt/2)×0.03t, 10sin(πt/2)×0.03t )で表される点は、こんな感じで大きな渦を描くことになります。ここまでは2次元平面での話。

3次元空間だと、さらにZの動きが加わることになります。

Z＝10cos(0.02πt)に設定。

点の軌跡が球体に沿うようにするには、Zが両端に来る時に軌跡が収束するように、X＝10cos(πt/2)×sin(0.02πt)、Y＝10sin(πt/2)×sin(0.02πt)と設定します。これで、球体の表面を沿うようならせん形を表現することができます。

もちろんX・Y・Zの媒介変数関数を複雑にすれば、より複雑な動きも表現できるようになるというわけです。

「一定の直径に対して一定の角速度を維持しながら、球体の表面上を一定の速度で移動する」という考え方は、円筒座標系に通じるものがあります。この球体と円筒座標系をリンクさせて作られるものの1つがメルカトル図法による地図です。