Aug 21, 2025 19:00:00

How to move an object in a spiral in 3D space?

Describing the movement of objects in 3D space requires an understanding of mathematics. ' Moving Objects in 3D Space ' is a website that uses animated slides to explain how to mathematically represent the trajectory of a point moving in a spiral along a round sphere.

Moving Objects in 3D Space

https://visualrambling.space/moving-objects-in-3d/

When drawing a spiral in 3D space, it's easier to imagine it as a point moving on the surface of a sphere. The 'Moving Objects in 3D Space' tutorial also uses animations to explain the process. Clicking or tapping on the right side of the screen advances the slide, and clicking or tapping on the left side moves back.

We consider 3D space as a three-dimensional Cartesian coordinate system, and consider the movement of a point by breaking it down into X, Y, and Z. For example, we express it as X=10cos(πt/2), where t is

a parameter . X is a simple cosine function, so it creates a beautiful wave like the one below.

Similarly, Y can be expressed as 10*cos(πt/2).

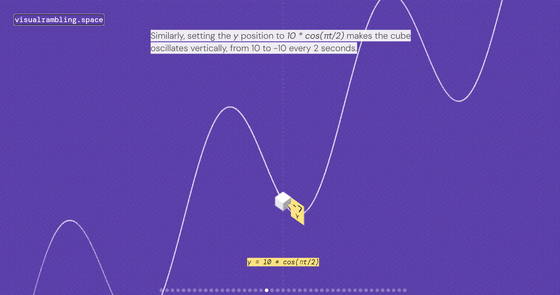
To represent a circle as the locus of points (X, Y), we need to express X and Y using trigonometric functions like this.

However, to represent a circle, set X=10cos(πt/2) and Y=10* sin (πt/2). This will make the point (X, Y) draw a circle with a radius of 10.

Next, let's set X = 10cos(πt/2) × 0.03t . With this function,

the amplitude of the wave will increase as shown below.

The same is true for Y = 10 sin(πt/2) × 0.03t .

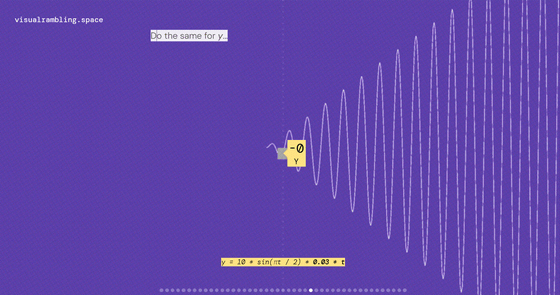
The point expressed as (X, Y) = (10cos(πt/2)×0.03t, 10sin(πt/2)×0.03t) will draw a large vortex like this. Up to this point, we have been talking about a two-dimensional plane.

In three-dimensional space, there is an additional Z movement involved.

Set Z = 10 cos(0.02 πt).

To make the locus of points follow the sphere, set X = 10cos(πt/2) × sin(0.02πt) and Y = 10sin(πt/2) × sin(0.02πt) so that the locus converges when Z reaches both ends. This will create a spiral shape that follows the surface of the sphere.

Of course, if you make the X, Y, and Z parameter functions more complex, you can express more complex movements.

The idea of 'moving at a constant speed on the surface of a sphere while maintaining a constant angular velocity for a constant diameter' is similar to the cylindrical coordinate system , and one of the things that link this sphere and cylindrical coordinate system is the Mercator projection map.