May 21, 2025 08:00:00

Is democracy mathematically impossible?

Veritasium, a YouTube channel that provides videos on various topics related to science and education, has released a video titled 'Why Democracy is Mathematically Impossible,' explaining the voting system in elections.

Why Democracy Is Mathematically Impossible - YouTube


The simplest method of elections in a democracy is to have voters choose one candidate on their ballot. This method is known as 'single-member constituency' and simply the candidate who receives the most votes wins. This method dates back to ancient times, having been used to elect members of the British House of Commons since the 14th century and is still used today to elect leaders in 44 countries around the world.

However, single-member constituencies have a problem: when choosing their parliamentary representatives, situations often arise where the majority of the country does not vote for the party that will be in power. In the past 100 years, there have been 21 instances when a single party has held a majority of seats in the British Parliament, but only twice did a majority of voters actually vote for that party. This means that parties with only a minority of support can come to power.

In addition, the single-member district system also leads to the phenomenon of 'similar candidates competing with each other for votes.' The 2000 US presidential election was essentially an election between Democrat Al Gore and Republican George W. Bush. At the time, every state in the US had single-member districts.

Bush won Florida by a very narrow margin, but the other candidate was Ralph Nader. Nader was the Green Party candidate, and was clearly more left-leaning than Gore and Bush. Nader argued that 'citizen concerns, people's concerns, the poor, the rich, the middle class, need to rise up against the power of special interests,' and won almost 100,000 votes in Florida. Some voters said, 'I don't know if I can conscientiously vote for Bush or Gore. I'm voting for Ralph Nader.'

However, the majority of voters who voted for Nader were surprised to find that Bush won instead of Gore. This is called the 'spoiler effect.' Most Nader supporters preferred Gore to Bush, but had no way of expressing their preference because the voting system only allowed them to vote for one candidate. Thus, single-member districts force voters to vote strategically.

The single-member district system is a winner-take-all voting system that leads to the concentration of power in larger parties and ultimately to a two-party system. This phenomenon of the convergence of the number of candidates in an election is called '

Duverger's Law .'

If single-member districts are problematic, what are the alternatives? One solution is to require that a candidate must receive a majority, i.e., at least 50% plus one vote, to win an election, and if no one receives a majority in an election, then those who voted for the candidate with the fewest votes are asked to vote for another candidate, and this process is repeated until one candidate receives a majority. However, holding multiple elections is a lot of work.

That's why there's the '

ranked voting' system, where voters are asked to rank candidates in order of their preference, and if their preferred candidate loses, they move on to the next choice. Once the polls close, the voters' first choices are tallied. If any candidate receives a majority of the votes, that candidate is declared the winner. However, if no candidate receives a majority, the candidate with the fewest votes is eliminated and their votes are allocated to the voters' second choices. This continues until one candidate receives a majority. Mathematically, it's the same as holding a repeat election, but it can save time and effort.

Ranked choice voting not only affects voters, but also how candidates behave towards each other. Ranked choice voting was used in the 2013 Minneapolis mayoral election. When the incumbent mayor stepped down, many people ran for mayor, and 35 candidates were lined up.

With 35 candidates, you'd think they'd all be attacking each other and trying to get attention, but instead, all 35 candidates were very kind and respectful to each other, so much so that at the end of the final mayoral debate, they all came together and sang a song together.

But ranked choice voting has a problem: a candidate's poor performance can actually help them win. For example, say you have three candidates: Einstein, Curie, and Bohr. Einstein and Bohr have very opposing views, and Curie is ideologically in the middle.

Now, suppose that after the vote, Einstein gets 25% of the votes, Curie gets 30% and Bohr gets 45%. Since no one has a majority, the round goes on to a second round where Einstein is eliminated. The people who voted for Einstein also chose Curie as their second choice, so Curie wins in the end.

Now suppose that Bohr gives a terrible election speech or proposes some very unpopular policies, and some of his supporters switch to Einstein's side. Now Curie drops out. Because she is a moderate, half of her supporters choose Einstein in the second round, and the other half choose Bohr. This makes Bohr win. In other words, Bohr's poor performance in the first round actually helps him win. This is a bad voting system.

This is something that French mathematician

Nicolas de Condorcet also thought about. Condorcet was one of the first people to rigorously apply logic and mathematics to the study of voting systems, and is one of the founders of a branch of mathematics called social choice theory . He was active during the French Revolution, when fair determination of the will of the people was a cultural preoccupation of the time.

In 1784, Jean-Charles de Borda of the French Royal Society of Sciences proposed a voting method in which voters were asked to rank the candidates. If there were five candidates, placing someone first would give that candidate four points. Second place would get three points, and so on, with the lowest ranking getting zero points. But the Borda method had a problem: the number of points given to each candidate depended on the total number of candidates. Adding extra people who had no chance of winning could affect the winner.

So in 1785, Condorcet published an essay in which he proposed a new voting system, called the 'Condorcet system.'

The Condorcet system requires that a winner beat all other candidates in a head-to-head election. But in practice, when there are many candidates, there is no need to hold many separate head-to-head elections. Instead, we ask voters to rank the candidates in order of preference, and then tally up the number of votes each candidate received higher than each of the other candidates.

For example, let's say three people are eating out and have three options: hamburger, pizza, and sushi. The first person has their preferences in the order hamburger]pizza]sushi, the second person has their preferences in the order pizza]sushi]hamburger, and the third person has their preferences in the order sushi]hamburger]pizza.

If the hamburger is chosen, the second and third person can argue that sushi should have been chosen instead, because only one of the three people has the same hierarchy: hamburger>sushi, and the other two have sushi>hamburger. However, by the same argument, pizza is preferred to sushi, and burgers are preferred to pizza. This leads to a circular argument.

This situation is known as the '

Condorcet Paradox .' However, before he could solve it, Condorcet himself was imprisoned for criticizing the new French government's new constitution, and died in prison.

Over the next 150 years, many mathematicians proposed their own voting systems or modifications of Condorcet's and Borda's ideas. Even

Lewis Carroll , author of the children's story Alice in Wonderland, tried to solve the problem under his real name, Charles Dodgson, but was never able to solve it.

In 1951, American economist

Kenneth Arrow published a paper titled “ Social Choice and Individual Values ”, in which he argued that a fair electoral system must meet the following five conditions:

Condition 1: Unanimity
If everyone in a group prefers one option over another, then the group as a whole should prefer that option too - for example, if everyone prefers sushi over pizza, then the collective decision should also prefer sushi over pizza.

Condition 2: Non-dictatorship
One person's preference should not dictate the entire decision. That is, if everyone votes for pizza and only one person votes for sushi, the group should choose pizza. If the decision rests solely on one person, it's a dictatorship, not a democracy.

Condition 3: Unlimited domain
The voting system must be able to handle any voting pattern: voters are free to rank any way they like, and the voting system must always produce the same result for the same set of votes, without skipping problematic votes or producing random results.

Condition 4: Transitivity
Collective preferences should be logically consistent: if a group prefers burgers to pizza and pizza to sushi, then they should prefer burgers to sushi. This ensures a consistent ordering.

Condition 5: Independence from irrelevant options
Group preferences between two options should not change depending on the presence or absence of other options. For example, the preference ranking between sushi and pizza should not change when a third option, a burger, is introduced.

However, Arrow proved that no voting system could satisfy all five of these conditions, which is known as

Arrow's Impossibility Theorem , and for which he was awarded the Nobel Prize in Economics in 1972.

So is democracy a mathematically impossible system? Arrow's Impossibility Theorem, which argues that 'when there are three or more candidates to choose from, there is no way to rationally aggregate voters' preferences,' seems to say so. However, in 1948, mathematician Duncan Black published a paper called '

Committee Decisions and the Rationality of Preferences ,' in which he presented the Median Voter Theorem . This Median Voter Theorem offers a more optimistic view than Arrow's Impossibility Theorem.

The median voter theorem, proposed by Black, states that when voters' preferences are distributed along a single political dimension, such as from left to right, and each voter's preferences are 'unimodal,' meaning that their preferences decrease the further away from a particular position, the preferences of the 'median voter' in the middle of the political spectrum will win in a majority vote.

The median voter theorem explains why political parties in many democracies tend to converge to the center, and shows that the severe constraints imposed by Arrow's impossibility theorem can be avoided under certain conditions, suggesting that democratic decision-making systems are not completely dysfunctional and can produce rational outcomes in the real world.

Arrow's Impossibility Theorem only applies to ordinal voting systems, in which voters rank some candidates above others. However, evaluative voting systems, in which voters express the degree of support they give to candidates rather than ranking them, are not bound by Arrow's Impossibility Theorem.

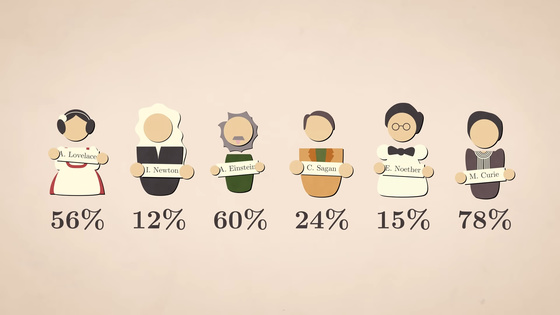
The simplest evaluative voting system is 'approval voting,' in which voters check all the candidates they support, and the candidate with the most approval wins. Research has shown that approval voting increases voter turnout, reduces negative campaigning, and prevents

the spoiler effect , in which third-party or minor-party candidates prevent ideologically close major candidates from winning.

Voters can express their approval of candidates without worrying about the size of the party they vote for. It is also easy to tally: just count the percentage of voters who approve of each candidate, and the candidate with the highest approval rating wins. Arrow was initially skeptical of the rating system, but later in life he acknowledged that it was probably the best way to go.

In fact, approval voting was used by Vatican priests to elect the Pope from 1294 to 1621, and it has also been used to elect the Secretary-General of the United Nations, but it is not widely used in large-scale elections.

Winston Churchill once said, 'Democracy is the worst form of government except all others that have ever been tried.' Veritasium responded, 'Democracy is certainly not perfect, but it is the best we have.'