What is Hilbert's Sixth Problem? It may have been solved after 125 years.

In March 2025, mathematicians Yu Deng, Zaher Hani, and Xiao Ma of the University of Chicago published a paper on the unpeer-reviewed paper repository arXiv, claiming to have solved Hilbert's Sixth Problem in fluid mechanics. The paper was still under peer review at the time of writing, but if Hilbert's Sixth Problem has truly been solved, it is said that physics has the potential to evolve significantly.
[2503.01800] Hilbert's sixth problem: derivation of fluid equations via Boltzmann's kinetic theory
Mathematicians just solved a 125-year-old problem, uniting 3 theories in physics | Live Science
https://www.livescience.com/physics-mathematics/mathematics/mathematicians-just-solved-a-125-year-old-problem-uniting-3-theories-in-physics
Hilbert's 6th problem is one of the problems presented by German mathematician David Hilbert in a lecture at the Second International Congress of Mathematicians held in 1900, and is called 'A mathematical treatment of the axioms of physics.'
Hilbert published a report in 1902 summarizing 23 problems (PDF file) , in which he states, 'The physical sciences in which mathematics plays an important role should be treated in a similar manner by means of axioms, among which probability theory and mechanics should be mentioned first. (Omitted) If geometry serves as a model for the treatment of the axioms of physics, we should first attempt to include as wide a class of physical phenomena as possible by means of a small number of axioms, and then, by gradually adding new axioms, arrive at more and more specialized theories.'

Simply put, physics is the science that explains the phenomena of the natural world. However, the methods and assumptions used to explain them can differ from person to person, or they can be ambiguous. For example, when calculating the speed of an apple falling from a tree, if you do not clearly state the assumptions, such as 'ignoring air resistance' or 'assuming the apple is a perfect sphere,' the answer will differ from person to person.
On the other hand, mathematics is an academic field that first abstracts things, then builds up strict definitions and logical proofs, and then clearly defines the scope of assumptions and definitions. Starting from the most basic assumptions, called axioms , various theorems are deductively derived to solve more complex propositions.
In Problem 6, Hilbert proposed that physics should also adopt this same mathematical rigor, by strictly defining basic concepts such as 'what is weight?' and 'what exactly is energy?', and then logically constructing a theory from there.

For example, the fluids around us, such as air and water, are made up of extremely small particles. The motion of each particle follows Newtonian mechanics , and if we know the position, mass, and velocity of each particle, we can simply calculate where they are at any given moment.
On the other hand, the motion of all particles, i.e., the fluid, is expressed by nonlinear equations of motion such as the Navier-Stokes equations , which are completely different from Newton's equations of motion. Fluid mechanics is based on the assumption of the concept of a continuum , and this assumption has not been proven by Newtonian mechanics.
One particular difference between Newtonian mechanics and fluid mechanics is 'time reversibility.' The microscopic physical laws of particles are time reversible , meaning that the laws hold even if time is run in reverse, whereas in the macroscopic world of the entire fluid, they are time irreversible, meaning that the equations no longer hold if time is run in reverse. In short, Newtonian mechanics and fluid mechanics are both fields of physics, but they are studied under different assumptions.
Hilbert's sixth problem asks whether the laws of motion for the entire fluid can be derived with mathematical rigor from the motion of particles that follow Newtonian mechanics. To solve this problem, Deng and his colleagues derived the Boltzmann equation , which describes the statistical behavior of particles, from Newtonian mechanics in a mathematically rigorous way.
In a fluid, countless particles collide repeatedly. In order to derive the Boltzmann equation mathematically and rigorously, it is necessary to track each and every particle collision, but if an infinite number of collisions occur, the calculations will never finish. It has already been proven that the number of collisions is finite in normal space, but in some spaces , the same particles may collide with each other multiple times, making it extremely difficult to evaluate the probability, so until now it has only been possible to derive it for very short periods of time.

Therefore, Deng et al. proposed the concept of a 'long bond' that connects two collisions that are sufficiently separated in time, making it possible to effectively analyze multiple collisions between the same particles. In addition, by introducing mathematical concepts such as 'layered cluster forest structure' and 'molecule,' Deng et al. claim that they have succeeded in deriving the Boltzmann equation more rigorously while dealing with 'arbitrarily long times.'
They then argued that by deriving the Boltzmann equation, which describes the distribution of particles, they were able to mathematically define density, momentum, energy, etc., and then derive the Euler and Navier-Stokes equations.
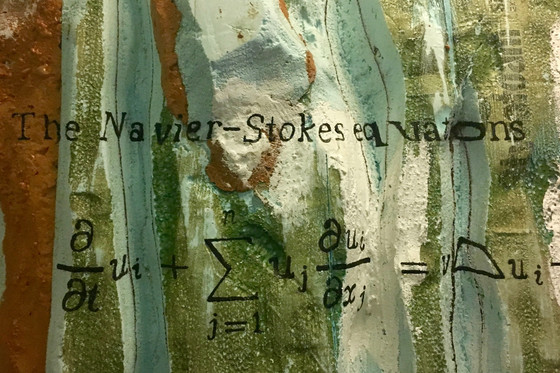
By Dan Updegrove
Regarding this paper, Deng et al. stated, 'The fundamental significance of this paper is that by deriving the time-irreversible Boltzmann equation from time-reversible microscopic Newtonian mechanics, we can clarify where the time irreversibility arises. ' In addition, by making the equations used in fluid mechanics mathematically more rigorous, it is possible that the reliability of simulations such as weather forecasting and aircraft design will improve.
The paper is currently under peer review, but if it is officially recognized as a solution, it will be a big step forward in both physics and mathematics. However, some experts have pointed out that there are 'serious flaws' and caution is required.
[2504.06297] Comment on 'Hilbert's Sixth Problem: Derivation of Fluid Equations via Boltzmann's Kinetic Theory' by Deng, Hani, and Ma
https://arxiv.org/abs/2504.06297
Related Posts:
in Science, Posted by log1i_yk