Apr 29, 2025 15:00:00

The algorithm 'Newton's method', which was invented by physicist Newton 300 years ago and is still in use today, is updated

by Alexander Borek

The

Newton method , invented by physicist Isaac Newton about 300 years ago, is an algorithm that still plays an important role in a wide range of fields, including logistics, financial engineering, computer vision, and pure mathematics. Many mathematicians have struggled to improve the Newton method, and recent research has finally updated it, according to Quanta Magazine, a science news site.

Implementable tensor methods in unconstrained convex optimization | Mathematical Programming
https://link.springer.com/article/10.1007/s10107-019-01449-1

Three Hundred Years Later, a Tool from Isaac Newton Gets an Update | Quanta Magazine
https://www.quantamagazine.org/three-hundred-years-later-a-tool-from-isaac-newton-gets-an-update-20250324/

Newton's method is a type of algorithm used for optimization, a mathematical tool used to find the 'lowest point' or 'best answer' of various laws.

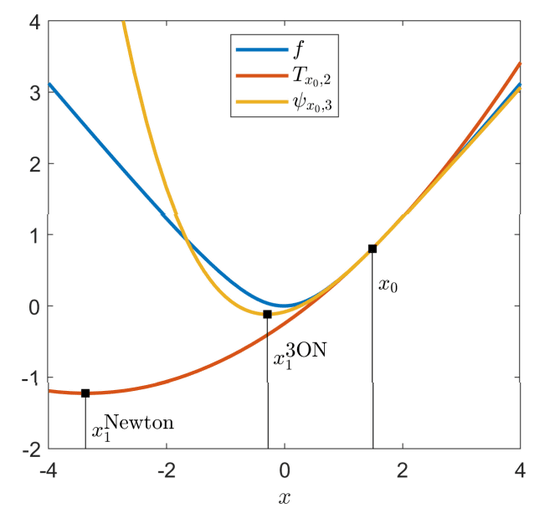
Around 1680, Newton realized that by performing a Taylor expansion using the first derivative f'(x), which indicates the slope of a function f(x) at a point x ₀ , and the second derivative f''(x), which indicates the curvature, he could derive a quadratic function 'f(x ₀ ) + f'(x ₀ ) * (x - x ₀ ) + (1/2) f''(x ₀ ) * (x - x ₀ ) ² ' that approximates _the original function f(x) around x 0. The Newton method involves repeating the same approximation using x ₁ , which gives the minimum value of this quadratic function, and then approximating again using x ₂ , which gives the minimum value of the quadratic function, and so on, until we approach the minimum value of the original function f(x).

Newton's method is not only found in the world of mathematics, but is also deeply involved in many technologies and problem solving that support our daily lives. For example, in GPS navigation, when finding the shortest route, it is necessary to calculate the route that is the shortest in time and distance from among various combinations of roads. Numerical analysis methods such as Newton's method are used to solve this 'optimization problem.'

It also plays an important role in the world of finance: investors use Newton's method to create portfolios of stocks, bonds, etc. that maximize profits while minimizing risk, and banks use similar mathematical methods to calculate interest rates on loans.

Furthermore, the development of self-driving car technology has also benefited from Newton's method. In image recognition, which processes large amounts of information from cameras and sensors and determines whether something is a pedestrian or a utility pole, algorithms like Newton's method are useful for efficiently optimizing functions with many variables. In addition, the ideas of Newton's method are used in a variety of other situations, such as the automatic focus function of cameras, the recommendation function of online shopping sites, and even the calculation of weather forecast models.

The greatest strength of Newton's method is its property called 'quadratic convergence.' This means that the error of the solution decreases exponentially with each iteration, and it can reach a solution in fewer iterations than algorithms such as

gradient descent . However, Newton's method has a weakness in that it does not work efficiently for all functions, especially complex non-convex functions. Therefore, mathematicians have been studying for many years how to expand the scope of its applicability while maintaining its efficiency.

In the 19th century, Russian mathematician Pafnuty Chebyshev proposed a variant of Newton's method that uses cubic equations to approximate functions, but Chebyshev's algorithm could only be applied to functions of a single variable.

In 2021, Russian mathematician Yuri Nesterov proved how to efficiently approximate functions with any number of variables with cubic equations. This was a major step forward, but it was not possible to extend it to higher-order equations of degree four or higher.

In 2024, a research team led by Professor Amir Ali Ahmadi of Princeton University and his former students Abrar Choudhury and Jeffrey Chang came up with a way to make a 'small adjustment' to the Taylor expansion using an optimization technique called 'semidefinite programming.'

Professor Ahmadi and his colleagues' method involves fine-tuning a function to have two important mathematical properties: ' convexity ,' which means that the function has only one valley, and 'sum-of-squares expressibility,' which means that the function can be expressed as a sum of the squares of multiple expressions. In other words, they solved the problem of 'wanting to use high-order approximations but having difficulty in calculations' by slightly adjusting the high-order approximations to make them easier to calculate.

This discovery made it possible to use higher-order Taylor expansions (third, fourth, or even fifth order or higher) to perform approximations, and the convergence speed was also improved dramatically. In a quadratic approximation, the error converges quadratically, and in a third-order approximation, the error converges cubically, so that an accurate answer can be reached with fewer iterations.

At the time of writing, Newton's method is computationally expensive, so gradient descent is still preferred for large-scale practical problems such as machine learning. However, Professor Ahmadi predicts that 'our algorithm is obviously faster in theory. In parallel with advances in computing technology, this theoretical advantage may be realized in practical terms in the next 10 to 20 years.'